At the start of the 20th century two new revolutionary and counterintuitive areas of physics were being developed, quantum mechanics and special relativity. While quantum mechanics describes the strange world of the subatomic with discrete energies, special relativity describes the effects of moving incredibly fast: time dilation and space contraction (general relativity is needed for a compete picture with mass warping spacetime).
In order to understand the dynamics of subatomic particles moving near the speed of light these two fields had to be united into quantum field theory. This was first done to describe the electromagnetic force, quantizing it into the theory of quantum electrodynamics (QED) which satisfies both quantum mechanics and special relativity. However to fully understand the atom, the strong force also needs to be quantized into quantum chromodynamics (QCD).
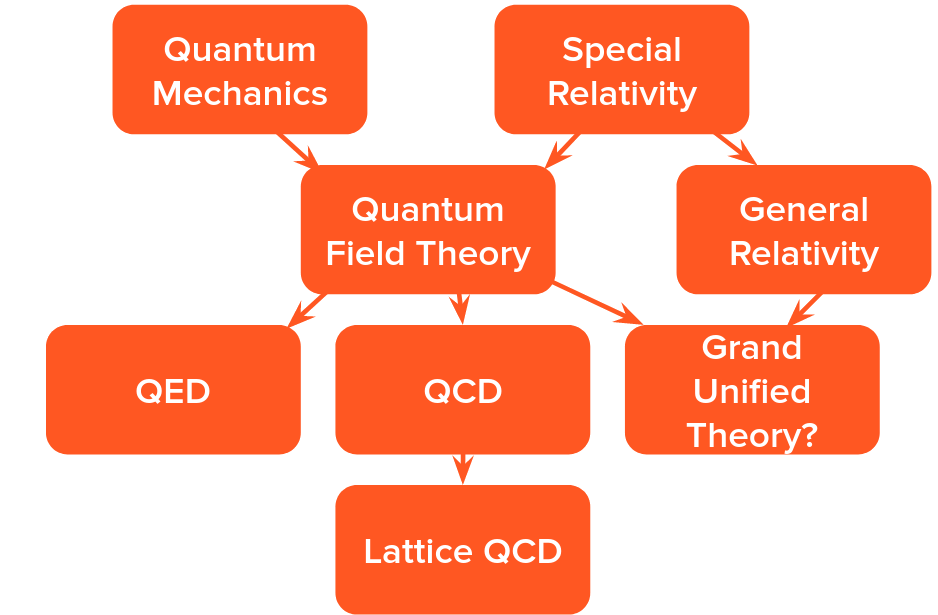
The strong force is what overcomes electric repulsion to hold protons and neutrons together in the nucleus, and binds quarks together to make up the protons and neutrons themselves. As the name implies, it is extremely strong compared to the electromagnetic force, which is why nuclei are able to be stable and not fly apart from the protons repelling each other (within certain limits).
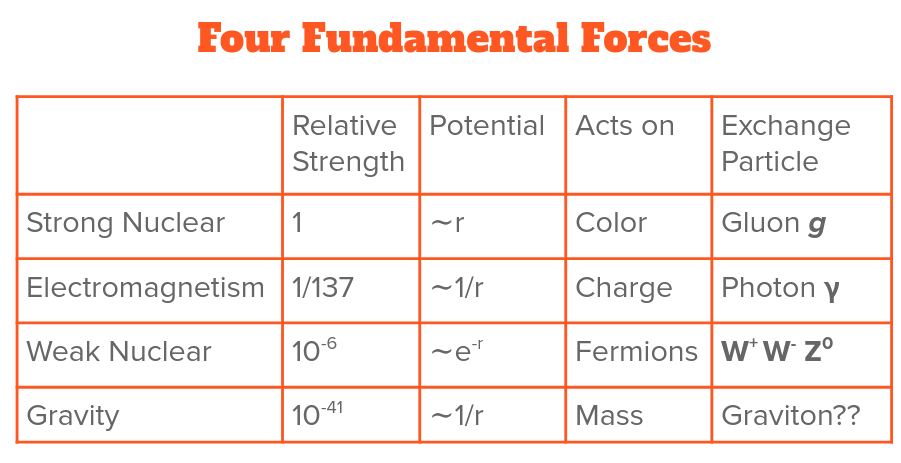
Similar to how the electromagnetic force only interacts with things that have electric charge (like protons and electrons, not neutrons), the strong force only interacts with things that have color charge. In the standard model of particle physics, which describes all currently known particles, the only particles that have color charge are called quarks and gluons. Gluons mediate the exchange of the strong force, and up and down quarks are what make up protons and neutrons, being “glued” together by gluons.

However, unlike electric charge which comes in 2 kinds (positive and negative), color charge comes in 6 varieties: red, green, and blue, as well as their creatively named opposites anti-red, anti-green, and anti-blue (sometimes referred to instead as cyan, magenta, and yellow respectively). While electric charge can be thought of as being on one axis, with negative being the opposite of positive, color charge has 3 axes, each with its own color and anti-color. The standard non-antimatter quarks can at anytime have any of the 3 colors, while antimatter quarks can have any of the 3 anti-colors, and a gluon has one color and one anti-color at all times.
When a particle is made up a quark and a anti-quark (called mesons), the anti-quark must have the anti-color of the quark. Likewise in a particle made up of three quarks (baryons) the quarks must have different colors, so a proton’s up and down quarks must be red, green, and blue, and a anti-proton must have anti-red, anti-green, and anti-blue anti-quarks. This is due to a concept called color confinement, quarks can not be observed on their own, and any particle made up of quarks must have a net zero (also called white) color charge.
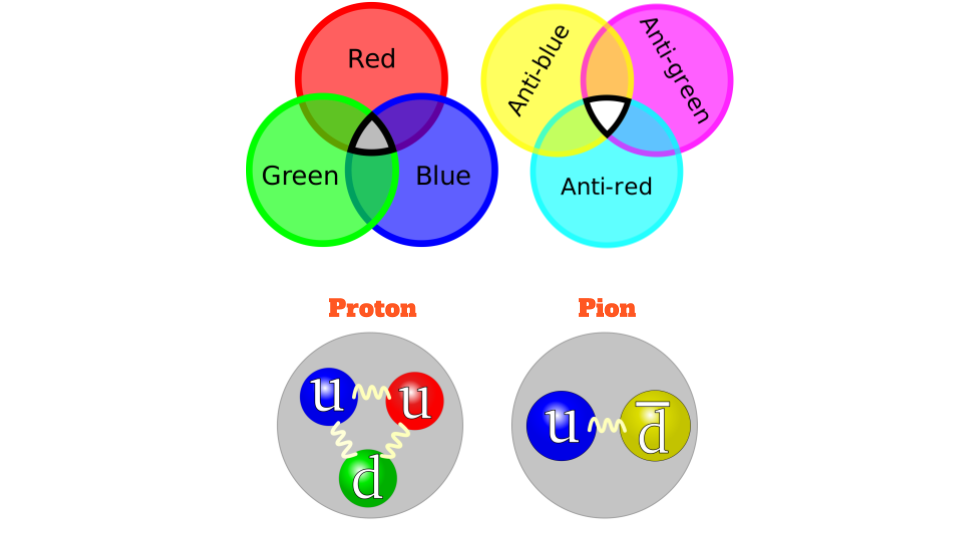
Color confinement is one reason why we do not see the strong force play a role in everyday life, at sizes bigger than a proton it looks like there is no color charge. Another reason is that the gluon particle has mass unlike the photon which mediates electromagnetism, meaning that it has a limited lifetime and so can only act on short distances very close to quarks.
It is also important to note that calling the strong force’s charge “color charge” is only an analogy and visual aid, it has no relation or connection to the physics of color.

Because of the probabilistic nature of quantum mechanics, to calculate quantum field theory problems you need to account for all the possible ways an interaction could happen. This usually entails summing over an infinite number of possible configurations, which is impossible. Quantum electrodynamics solves this problem using perturbation theory, it can approximate a calculation by only including the most likely configurations. The more increasingly less-likely configurations you include the more accurate the calculation is.
This works in QED because the electromagnetic coupling constant is less than 1, so more complicated configurations with more interactions contribute less and less to the final answer. However the strong force’s coupling constant is 1, meaning that every possible way an interaction can happen is equally as likely. This makes it impossible to approximate the most likely scenarios using this method.
In order remove this infinity and allow QCD problems to be calculated, space and time are instead discretized into a finite 4D grid. In this grid each point represents the quark field, and the lines connecting them represent the gluon field.
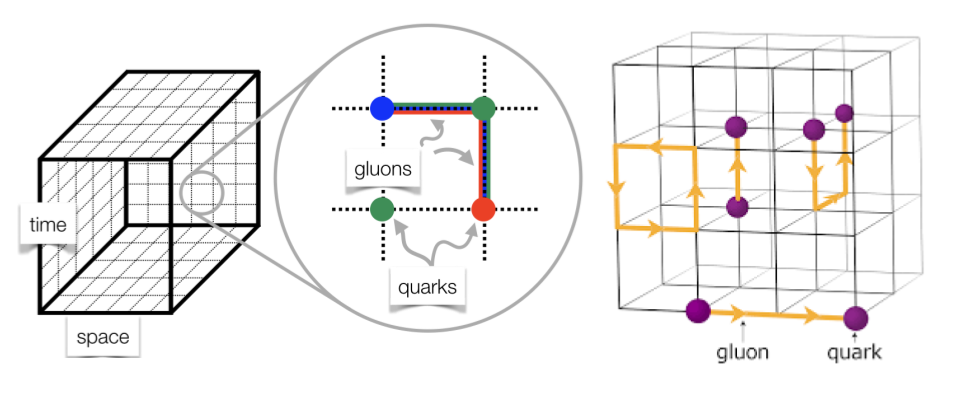
Although this gets around the infinite possible configurations, it is still an extremely large problem. To reduce the complexity further so it can be computed in a reasonable time a Monte Carlo algorithm is utilized. Monte Carlo is a method of using random sampling to approximate a problem, it has many applications to problems in biology (see here for it used in protein folding), math, and physics. Monte Carlo is best demonstrated as seen below to approximate the value of pi by seeing if a random point lies within the circle or not, with the more random points the closer to the true value you get.
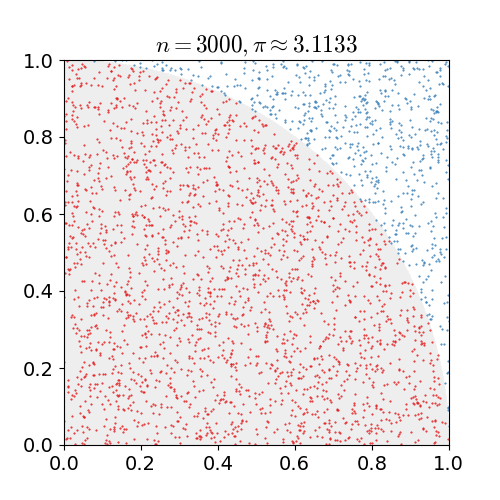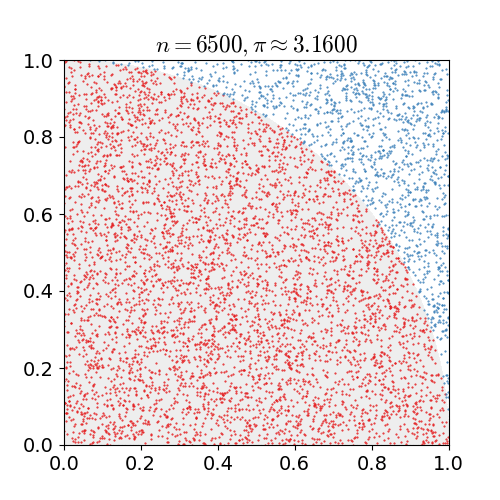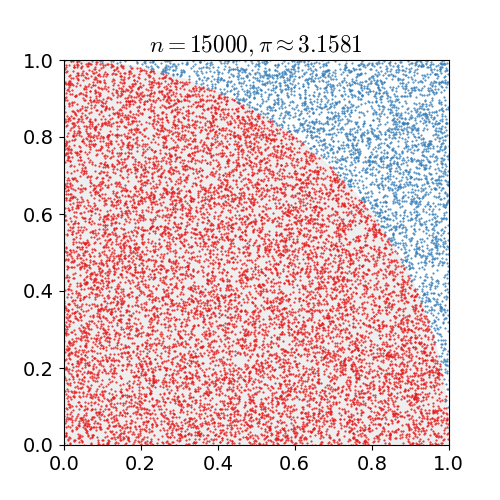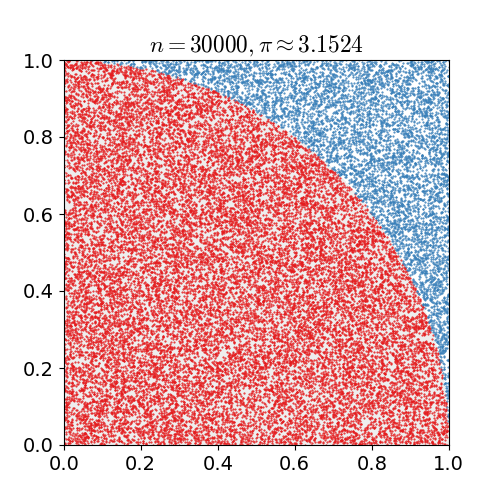
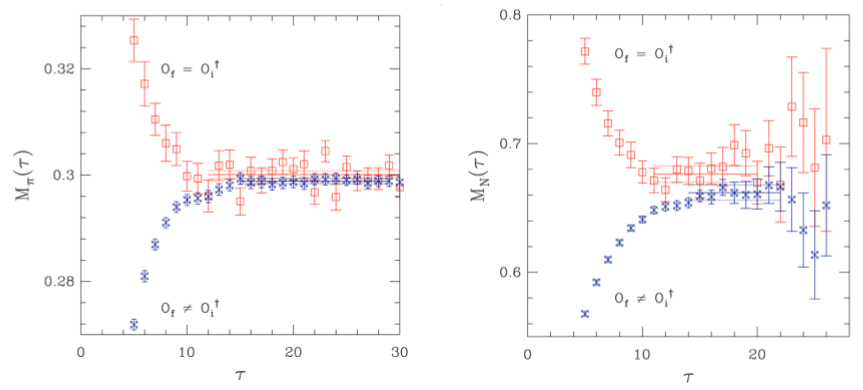
Now with lattice QCD it is possible to preform calculations and make predictions about quarks and nuclei, such as the mass of mesons and baryons. The graph on the left below shows two different lattice QCD methods converging to the same mass for a pion, which very closely matches the experimentally measured mass. However the graph on the right shows what happens when this is applied to predict the mass of a neutron, they converge to a mass before diverging again. This divergence is due errors in the Monte Carlo approximation compounding together, creating a small golden window with the correct mass before error takes over.
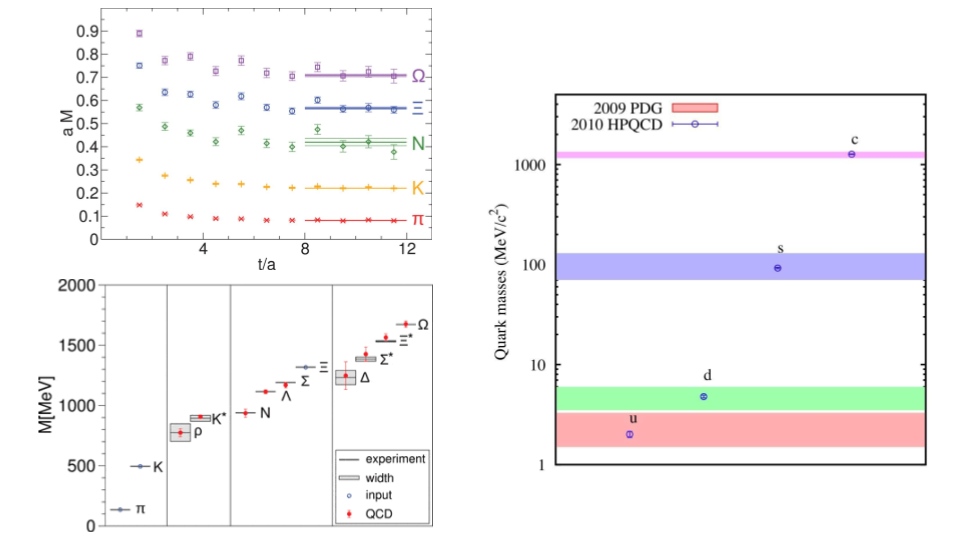
Lattice QCD can be used to solve countless problems in particle and nuclear physics, such as the very accurate mass predictions for more hadrons and quarks as seen below. There has also been a lot of progress in the last 10 years utilizing it to understand QCD decay constants, resonances, deep inelastic scattering, QCD phase transitions, and investigating color confinement.
This article is based on a presentation I gave in 2020, see the full slides here.